In music, a ghost note, dead note, or false note, is a musical note with a rhythmic value, but no discernible pitch when played. On stringed instruments, this is recognised by the sound of a muted string. Muted to the point where it is more percussive sounding than obvious and clear in pitch. There is a pitch, to be sure, but its musical value is more rhythmic than melodic or harmonic… (source = wikipedia)
Until now I haven’t been confronted with severe dead notes problems yet. I have experienced the phenomenon a couple of times, but not at such a degree that my clients have asked me to intervene.
But it happens that one of my wife’s sitars suffers from this, and recently an extra occasion came with this mail by Toss Levy: “… Dead notes on a sitar have always been a problem. Mostly by careful jawari and work on the taraf bridge and strings, I could get a better resonance. I have found dead-notes to be on most instruments and consider the instruments with a responsive resonance over the entire note range rare but of super quality. For me, and maybe in my ignorance, I have accepted the dead-notes as a sign of a lesser quality instruments… How does one go about solving the dead-note problem ??…” :
From my school-time I always remember an important basic physics law about acoustic resonance (source = wikipedia):
k = stiffness
m = mass
ωn = radian frequency (radians per second)
From the radian frequency, the natural frequency, fn, can be found by simply dividing ωn by 2π. Without first finding the radian frequency, the natural frequency can be found directly using:
k = stiffness (Newtons/meter or N/m)
m = mass(kg)
fn = natural frequency in hertz (cycles/second)
This equation tells me that the resonance frequency is proportional to the stiffness and inversely proportional to the mass of an acoustic system. It sounds logical, and gives us a rather simple tool to influence the phenomenon:
Working on the stiffness includes interfering in the instruments basic wooden construction: tabli, tumba, neck, joint etc. … 
But this is uttermost time consuming and almost impossible to experiment with, and surely not, on an expensive well-built sitar.
But working on the mass can be done very easy: I did some experiments on adding mass to the ghodi (jawari – bridge construction) and the result is very promising. I have prepared and selected a couple of metal parts (lead) ranging from 10g, 20g, 30g,… to 150g and attached these one by one to the ghodi. And as the formula predicts, the resonance frequency is really shifting down. In my case, with 30g added, from komal GA towards main tonic SA where the amplitude of the resonance has been reduced such that it is almost not heard anymore.
Results (sound samples):
1: Play original jawari (nothing added)
2: Play jawari + 10 grams added
3: Play jawari + 20 grams added
4: Play jawari + 30 grams added
5: Play jawari + 50 grams added
6: Play jawari + 100 grams added
7: Play jawari + 150 grams added
Comments on the results:
1: Dead note is clearly heard on komal GA, also noticeable on GA. (Never mind the missed NI…).
2: Dead note is already reduced in amplitude and slightly shifts towards RE.
3: Dead notes amplitude is even more reduced and shifts over RE.
4: Dead note is now almost disappeared, reaching SA.
5: Dead note is now completely gone, but the overall sound is losing low frequency range because of the damping effect of the weight.
6 & &7: The overall sound loses more and more low frequencies because of an increased damping effect.
Some considerations:
Adding a weight to the jawari can be compared to the act of adjusting a kind of acoustic audiofilter. This implicates that when talking about acoustic waves there are always 3 parameters to keep in mind: fo, the frequency itself; A, the amplitude (how strong is the influence) and Q, the quality factor which is related to Δf, the bandwidth. This means that adjacent frequencies are involved in the proces. 
The lower the quality factor, the bigger influence will be noticeable on adjacent notes or srutis too. This one can be determinative for the result.
Unfortunately it is not a linear but an exponential equation. The result of the operation becomes stronger and stronger OR lesser and lesser at an exponential rate… This means that the practical adjustable range will be limited, and probably difficult to measure. Trouble might be to find a good starting weight. But, patience is a golden virtue…
Harry Shaffer, a creative sitar maker living in Asheville, North Carolina, USA, has been developing an all carbon fiber acoustic sitar over the past couple of years. He began designing plywood guitars as a child and discovered his fascination with the sitar and the music of India in 1993. Because of his frustrating experiences with his first no-name sitar, he put his lutherie skills to work and began ripping sitars apart in order to figure out how to make them work better. In 2013 he founded Carbon Sitars and he actually begun taking orders for custom made carbon fiber acoustic sitars.
This extraordinary version called “The Suibokuga Sitar” was inspired by the art of Japan, in particularly, the sumi-e, or ink wash painting. The main pegs lack the traditional sitar designs, opting for a more Japanese design.
Here is a concept drawing of the main bridge. Harry Shaffer wanted something that reflected the aesthetic of Japanese architecture, so he chose a design that invokes a “torii” or gate to a Shinto shrine.
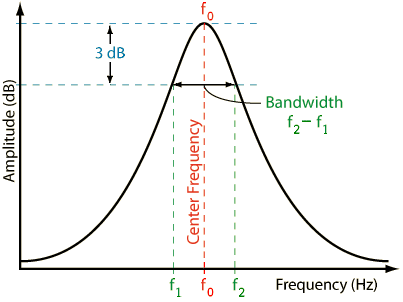Adding a weight to the jawari can be compared to the act of adjusting a kind of acoustic audiofilter. This implicates that when talking about acoustic waves there are always 3 parameters to keep in mind: fo, the frequency itself; A, the amplitude (how strong is the influence) and Q, the quality factor which is related to Δf, the bandwidth. This means that adjacent frequencies are involved in the proces. 
The lower the quality factor, the bigger influence will be noticeable on adjacent notes or srutis too. This one can be determinative for the result.
